电化学储能技术因能量密度大、占地面积小、噪音低、建设周期短,已经成为最具市场前景的储能技术。根据中国太阳能行业协会(CPIA)统计数据,截至2019年底,全球累计电化学储能装机达8.22 GW,同比增长24.02%,其中,用户侧储能占比最高,为28%;我国电化学储能累计装机1592.3 MW,同比增长48.4%,用户侧仍是储能最大的应用市场,占比为51%。从以上数据可以得出,用户侧电化学储能占据了重要的市场份额,因此对于用户侧电化学储能的应用研究非常必要。
目前对用户侧储能研究主要集中在系统经济性研究,文献针对不同电池储能技术路线进行分析,研究其性能指标及制约影响因素;文献主要研究了用户侧储能不同安装地点对用户供电可靠性指标影响,同时制定充放电策略,对比两种策略下的收益、装置寿命及经济性。文献[7]通过建立经济运行模型,研究了区域型电网中储能系统的经济效益。文献[8]通过预设恒定充放电功率和削峰填谷控制目标,计算系统最优配置,由于预设条件,受到人员经验的影响,寻优过程是在局部完成,所得系统配置并非是全局最优配置。文献[9]研究了综合能源配网的储能系统配置方法。
用户侧削峰填谷储能装置的经济性主要由初期投资和装置收益决定,初期投资受储能系统成本、系统配置、政策等因素影响;装置收益由储能系统配置、系统充放电策略、地区峰平谷差价、用户的电负荷大小和特征、系统效率、电池循环次数、电池充放电深度等因素决定。目前缺少基于用户负荷分析结果的最优的储能系统配置和充放电策略计算方法,系统配置主要根据经验设定,充放电策略也是人为预设,以此设计出的储能装置并不能保证经济性最优。
本文建立用户侧电化学储能系统经济模型,以装置经济性最优为目标,采用遗传算法,对系统配置(系统额定容量和额定充放电功率)及系统充放电策略进行双层优化计算;借助建立的模型,分别计算两种收益模式下储能装置最优系统配置、系统充放电策略及系统经济性分析。
1 用户侧电化学储能系统收益模式
1.1 大工业用户两部制电价
对于大工业生产用电,变压器总容量在315 kV·A以上执行“两部制电价”。所谓两部制,一部分是基本电价,一部分是度电电价;基本电价是以企业受电容量(kV·A)或企业最大需量(kW)计算的[式(1)、式(2)],称为容量费或需量费,不管企业是否用电,都需要缴纳,并与实际用电量无关;受电容量指的是企业变压器容量,最大需量是指根据实时监测的最大用电功率(每15 min采集的电负荷的最大值);度电电价是用户实际消耗电量对应的电价,包含尖、峰、平、谷时段的电价总和。
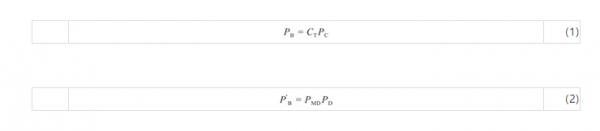
式中,CT为变压器容量,kV·A;PMD为企业月最大需量,kW;PC为容量计费单价,元/(kV·A·月),PD为需量计费单价,元/(kW·月)。
1.2 削峰填谷收益
在用户侧设置一定容量的储能装置,理论上在电价谷段、平段时从电网向储能装置充电,在电价尖峰、峰值时段储能装置向电网负荷放电,考虑充放电效率,通过削峰填谷可为企业节约一部分度电电费,降低企业用电成本。
1.3 需量调节收益
通常情况,用户采用变压器容量计费模式,当变压器长期处于低负载运行状态时,可以进行基本电费容改需缴费模式调整,即基本电费从变压器容量计费改为最大需量计费;在用户侧设置一定容量的储能装置,一方面实现削峰填谷,另外一方面可以实现需量调节,即削减企业最大需量负荷,削除不稳定的过负荷冲击,降低企业的月最大需量,从而为企业节约一部分基本电费,进一步降低用电成本。
2 用户侧电化学储能系统经济模型
2.1 目标函数建立
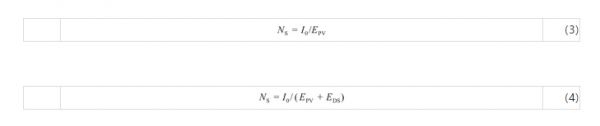
式中,NS为储能系统回收期,年;式(3)中的NS是削峰填谷模式下的系统回收期,式(4)中的NS是削峰填谷+需量调节模式下的系统回收期;I0为储能系统初期投资成本,元;EPV为储能系统年峰谷收益,元/年;EDS为年需量调节收益,元/年。
2.2 年峰谷收益

式中,PL(t)为原电力系统逐时负荷,kW;PEL(t)为t时刻电价,P尖、P峰、P平和P谷分别代表尖、峰、平、谷时段的用电单价,元/(kW·h);PS (t)为储能系统t时刻的充放电功率,kW;ηS (t)为储能系统t时刻充放电效率。
2.3 年需量调节收益
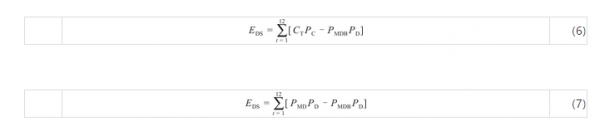
式中,PMD为设置储能系统前的月最大需量,kW;PMDB为设置储能系统后的月最大需量,kW。
若用电企业的基本电费采用容量计费模式,首先实施容改需调整,并通过设置储能装置削峰填谷后,需量调节收益可采用式(6)进行计算;若用电企业的基本电费采用需量计费模式,通过设置储能装置削峰填谷后,削减最大需量,需量调节收益可采用式(7)进行计算。
2.4 年初期投资成本
不考虑贴现率
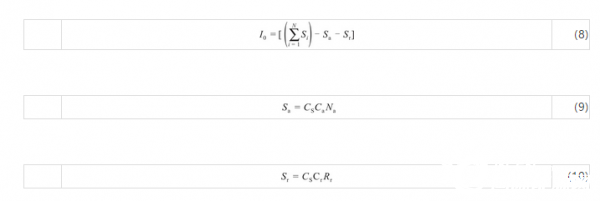
式中,为储能系统各子系统(包含电池、PCS、BMS、EMS、辅助系统)成本、电缆材料、土建施工等总投资;Sr为电池回收成本,元;Sa为政策补贴收益,元;Ca为补贴单价,元/(kW·h·年);CS为储能系统容量,kW·h;Na为补贴年限,年;Cr为电池回收单价,元/(kW·h);Rr为电池成本回收百分比,目前,铅碳电池的回收成本百分比取25%,磷酸铁锂为0。
2.5 模型约束条件

式中,T≥1/V。
其中,为电化学储能系统的额定充放电功率,kW;PLmax为电力系统负荷最大值,kW;CTF为变压器剩余容量,kV·A;DOD为电池放电深度;为储能系统日循环次数,次;T为储能系统充放电时间,h;V为电池充电倍率。
3 案例分析
采用遗传算法,求解上述模型。分别计算不同收益模式对应的最优系统配置、最优运行策略以及回收期。表1是苏州某大工业用电企业(用电等级:1~10 kV)典型日逐时负荷,企业变压器信息见表2,苏州地区尖、峰、平、谷电价及时段见表3、表4;企业典型日逐时负荷曲线与电价曲线如图1、图2所示。
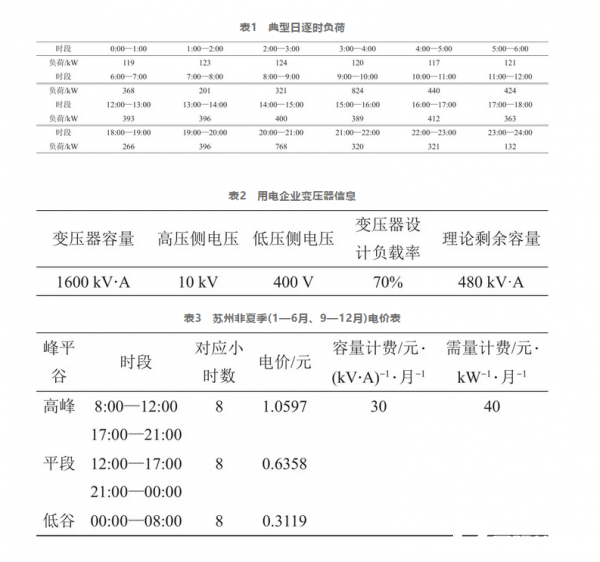
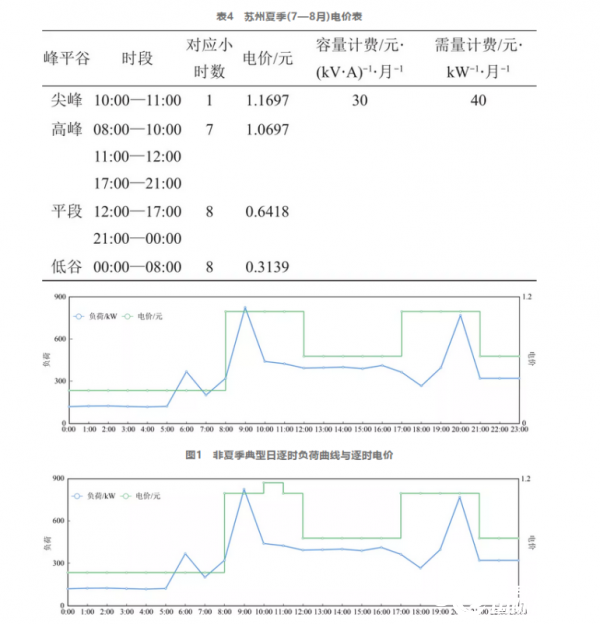
案例1针对上述苏州用电企业电价信息、典型日逐时负荷,选用磷酸铁锂电池(主要参数见表5),计算削峰填谷模式下的系统最优配置和最小回收期,结果见表6,系统最优运行策略如图3~4所示。


因江苏地区夏季存在尖峰电价,因此典型日按照夏季、非夏季两种情况考虑。按照上述条件计算出的系统最优额定容量为821 kW·h,系统最优额定充放电功率为144 kW,系统每日循环次数为1.4次,装置年限为9.5年,实际每日充放电量为1149.4 kW·h,装置回收期为7.1年。非夏季,无尖峰电价时,系统最优运行策略如图3所示,在谷段充电约5 h(0:00—4:00),充电功率为144 kW,荷电状态由10%变到100%,电池充满;在峰段(8:00—11:00)放出电量,荷电状态由100%变到40%,在平段电池继续充电,荷电状态由40%变到75%,在第2个电价高峰,电池继续放电,直到荷电状态恢复到最初10%;在夏季,系统最优运行策略如图4所示,因存在尖峰电价时段(10:00—11:00),系统在该时段的放电功率为140 kW,图4系统在峰段(8:00—11:00)荷电状态由100%变到37%,较图3倾向于放出更多电量,获得更多收益。
通过模型参数导入,逐时电负荷分析、约束条件限制,将系统额定容量、系统额定充放电功率、系统逐时充放电功率作为变量,以系统回收期最小为目标,采用遗传算法寻优计算得到案例1的最优系统配置和最优运行策略,为储能系统优化设计提供准确的计算方法;对于含有尖峰电价的地区,考虑了尖峰电价对系统配置及运行策略的影响,基于负荷特征分析制定不同典型日运行策略,实现年峰谷收益最大。
3.2 用户侧储能装置削峰填谷与需量调节模式下的系统最优配置及最优运行策略
案例1只考虑峰谷收益,为提高储能系统收益,降低系统回收期,案例2在案例1的基础上增加需量调节收益,在储能系统削峰填谷的基础上,削减最大需量负荷;在采用遗传算法寻优过程中,系统最优配置和最优运行策略将是使得系统投资最低,峰谷收益和需量调节两部分收益总和最大的那组结果。
案例2最优系统配置计算结果见表7,系统最优运行策略如图5~6所示。

考虑削峰填谷与需量调节收益模式,按照上述条件计算出的系统最优容量为821 kW·h,系统最优额定充放电功率为144 kW,系统每日循环次数为1.35,装置年限为10年,每日实际充放电量为1108 kW·h,装置回收期为6.2年。对比案例1结果,案例2储能系统回收期缩短,主要原因是增加了需量调节收益。由逐时负荷数据提取用户最大需量为824 kW,出现在典型日9:00—10:00之间;从运行策略图可以看出,不管是非夏季还是夏季,该时段放电功率均为最大放电功率,最大程度削减用户的尖峰需量值,削减后最大需量值为684 kW,每年节省需量电费为6.72万,系统回收期由7.1年缩短到6.2年,提高了系统的经济性;图5和图6中,其尖峰时段(10:00—11:00)放电负荷均为系统最大的放电功率,即图5和图6均得到了此系统配置下的最大值峰谷收益和需量收益。
4 结 论
(1)通过建立用户侧电化学储能系统经济模型,以装置经济性最优为目标,采用遗传算法,以系统额定容量、系统额定充放电功率、系统逐时充放电功率作为变量进行寻优计算,不断交叉变异,得到一组最优解,即最优配置和最优运行策略满足系统回收期最小,为用户侧储能系统配置设计及策略制定提供了准确的方法,同时准确提供系统的经济性用以项目决策,为储能技术市场推广提供必要条件。
(2)通过对比不同收益模式下的储能系统配置及经济性,得出同时考虑削峰填谷和需量调节收益模式进行储能系统配置设计,系统最优配置与削峰填谷模式下的配置相同,系统最优充放电策略发生改变,在逐时负荷尖峰处,以额定放电功率放电,最大程度削减最大需量值,系统回收期缩短,经济性提高,为储能技术的大规模商业化推广提供有利条件。
(3)两种收益模式下,采用遗传算法计算的储能系统最优策略均为谷段充满,荷电状态变化范围为10%~100%,峰值时段放出部分电量,平段继续充电,第二峰值时段放电至荷电状态为10%,实现充满放完;在夏季尖峰时段,以额定放电功率进行放电,实现峰谷收益最大;基于系统运行策略而计算的最优系统容量,实际日充电量为1.5倍左右的系统可充容量;该结论可为类似储能系统配置设计及策略制定项目提供参考依据。
 切换行业
切换行业

 正在加载...
正在加载...




