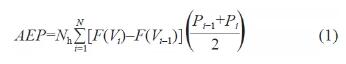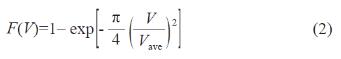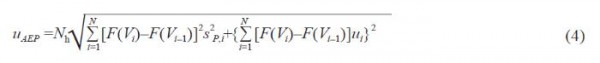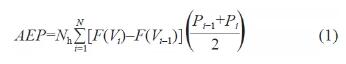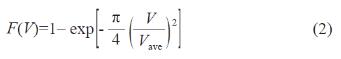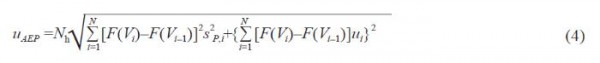在充分研究了IEC 61400-12-1 标准中关于
风电机组年发电量计算方法的基础上,结合概率论的相关理论,对该标准中计算方法存在的缺陷进行了分析,提出了一种优化算法,并对优化算法和标准算法的计算结果进行了对比分析。结果表明,在相同置信区间内,采用优化算法计算的年发电量结果的不确定度更低。
功率曲线是评价
风电机组发电性能的重要指标之一,而年发电量的计算作为功率特性测试结果应用的一个具体体现,是验证风电机组发电能力的主要技术指标,特别是在机组出质保过程中,年发电量作为一个重要的考核指标,越来越受到业主和整机厂的重视。
为了验证风电机组的实际发电性能,目前业界普遍采用的一种方法是按照IEC 61400-12-1《Wind energy generation systems-Part 12-1: Powerperformance measurements of electricity producingwind turbines》[1] 规定的程序,对已经安装运行的风电机组的输出功率和入流风速等参数进行测量,然后利用Bin 法得到该机组的实测功率曲线[2],再根据得到的功率曲线和风速分布计算机组的理论年发电量,得到的计算结果将作为最终评价风电机组发电能力的主要指标。因此,如何准确计算风电机组的年发电量成为各方关注的焦点。本文重点研究了IEC 61400-12-1 标准中关于
风电机组年发电量的计算方法,在此基础上结合相关理论对标准算法进行了优化,并对优化算法和标准算法的结果进行了对比分析。
01
基于IEC 61400-12-1年发电量计算
在IEC 61400-12-1 标准中,针对风电机组年发电量的计算( 下文简称“标准算法”) 通过以下方式实现。首先,将测试所得的所有数据剔除无效数据,然后利用Bin 法得到该风电机组的实测功率曲线;在基于假设风速符合瑞利分布的条件下,利用该功率曲线和该风场的年平均风速,结合风速的区间概率计算出等效的平均功率;最后用该平均功率再乘以全年的等效小时数8760 h,即可得到被测风电机组的理论年发电量。
在实测功率曲线的统计过程中,IEC 61400-12-1 标准做了以下规定:以风速为参考,按照0.5m/s 的整倍数进行区间划分,且每个区间以0.5m/s 的整倍数为中心值,按照前后各0.25 m/s 进行连续划分[1-6],区间为前闭后开,划分完成的每个风速区间可表示为[Vni–0.25, Vni+0.25),其中,Vni 为该区间的中心风速。例如3.5 m/s 这个风速点,代表的风速区间为[3.25, 3.75)。然后对每个风速区的风速和对应功率分别统计平均值,统计结果即为实测功率曲线。
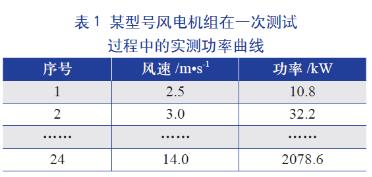
表1 为某型号风电机组在一次测试过程中得到的实测功率曲线,测试时空气密度为1.225 kg/m3,场地的年平均风速为6.4 m/s。
根据IEC 61400-12-1 标准的规定,在确定了实测功率曲线以后,采用式(1) [1-6] 和相应的初始条件进行理论年发电量AEP的计算。
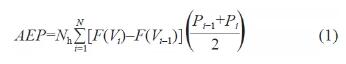
式中,Nh 为一年中的发电小时数,取值为8760 h;N 为功率曲线的区间个数;F(V) 为风速的瑞利累积概率分布函数;Vi 为第i 个区间标准化的平均风速,m/s;Pi 为第i 个区间的平均输出功率,kW。
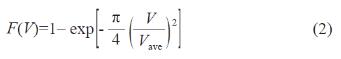
式中,Vave 为轮毂高度的年平均风速,m/s;V 为风速,m/s。
在利用式(1) 计算的过程中,需要进行初始条件假设,具体假设为:V0=V1–0.5 m/s,P0=0kW[1,3-6]。从式(1) 可以看出,理论年发电量的计算是按照实测功率曲线上2 个连续的风速点来划分风速区间的,而相应区间的功率平均值则用2 个端点的平均值来表示。从实测功率曲线计算的过程来看,显然这个功率平均值不能表征该风速区间的实际功率平均值。这个误差将导致计算得到的理论年发电量和实际年发电量存在较大偏差,并且由于初始条件的假设,引入了额外的计算不确定度。
同时,基于式(1) 和不确定度表示方法的相关规定,IEC 61400-12-1 标准给出了年发电量计算结果的不确定度uAEP 的计算方法[1-6] 为:

式中,fi=F(Vi)–F(Vi–1);sP,i 为实测功率曲线上功率的A 类标准不确定度;ui 为实测功率曲线上功率的B 类标准不确定度。
为了和理论年发电量的计算公式统一并便于后面的分析,将式(3) 改写为式(4) :
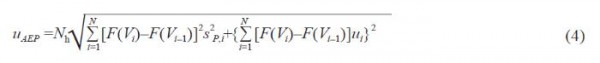
式(4) 中相关变量的计算方法和确定依据在IEC 61400-12-1 标准中有详细的论述,本文不再对其进行分析。需要特别指出的是,在使用该公式时,由于fi=F(Vi)–F(Vi–1) 的存在,在计算过程中也需要进行初始条件假设,即在i=1 时引入初始条件V0=V1– 0.5 m/s,而该假设条件的引入也会导致不确定度计算结果额外的偏差。
为了得到更准确的理论年发电量及实现对不确定度的准确评估,本文在研究了实测功率曲线的形成过程和年发电量计算原理的基础上,对年发电量的计算公式和边界条件进行了优化( 下文简称“优化算法”) 。
02
基于优化算法的年发电量计算
标准算法在计算风电机组的理论年发电量之前,首先需要根据测试数据得到其实测功率曲线,然后按照该功率曲线和风速的概率分布计算得到每个风速区间的功率估计值。因此,各风速区间功率估计值的计算是年发电量计算过程中的关键。
标准算法在计算风速的区间概率时,需要根据实测功率曲线重新进行风速区间划分,使用连续2 个Bin 区间的统计中心值形成新的年发电量计算风速区间[Vi–1,Vi),使用该区间上2 个风速在实测功率曲线上对应的算数平均值作为该区间的平均功率。而考虑到实测功率曲线的非线性特征,使用该平均功率很难准确表示出对应风速区间的功率均值。
通过对实测功率曲线计算流程的分析不难发现,在最终得到的实测功率曲线上,每个点都已经带有区间属性。例如表1 中实测功率曲线上的点(3.0 m/s, 32.2 kW) ,其代表的是风速区间[2.75,3.25) 的计算结果。因此,结合概率论的知识和年发电量的计算原理,可将式(1) 优化为:

由式(5) 可知,优化算法使用的就是实测功率曲线上的点,无需初始条件的假设,可避免因为引入初始条件而导致的计算误差。
同时基于本文的改进方法,在年发电量不确定度的评估公式方面,虽然仍沿用式(3) ,但是其计算条件却发生了变化。优化算法计算时取fi=F(Vni+0.25)–F(Vni–0.25),无需引入计算初始条件V0=V1–0.5 m/s,从而保证了计算公式本身的完整性,避免了因计算初始条件假设引入的计算误差。
根据表1 所示的实测功率曲线数据,利用优化算法计算得到该风电机组的年发电量及不确定度,并将计算结果和标准算法的计算结果进行比较,对比如表2 所示。表中,测试时的空气密度为1.225 kg/m3,场地的年平均风速为6.4 m/s。
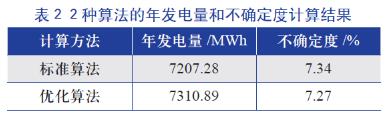
从表2 的计算结果可以看出,使用优化算法计算出的结果的不确定度较标准算法略低。
03
结语
本文在IEC 61400-12-1 标准中关于实测功率曲线统计和年发电量计算方法的基础上,结合概率论的相关知识,对标准算法进行了优化改进。通过对比分析表明,优化算法能够更加准确地给出年发电量的计算值,且在计算过程中无需进行初始条件的假设,在保证计算公式本身完整性的同时,也使算法变得更加简便。